1.理解正方形的基本属性 正方形是一种四边相等的矩形,其对角线互相平分且互相垂直。因此,我们可以使用勾股定理来解决这个问题。假设正方形的边长为$a$(以米为单位),则其对角线长度为$asqrt{2}$。由于面积等于边长的平方,我们有: [ text{面积} = a^2 ] [ 10 = a^2 ]
2.解方程求边长 现在我们有了面积和边长的等式,我们可以将其转换为关于$a$的方程。将已知条件代入方程: [ 10 = a^2 ] 为了找到边长$a$的值,我们需要对方程进行开方处理。取平方根,得到: [ a = sqrt{10} ]
3.计算具体数值 现在我们已经得到了正方形的边长,但是我们需要将它转换成实际的长度单位。假设我们使用米作为度量单位,那么: [ a_{text{米}} = sqrt{10} approx 3.16 , text{米} ]
4.举例说明 假设有一个实际的正方形场地,它的边长为3.16米。那么它的面积就是: [ text{面积} = (3.16 times 3.16) = 10.0952 , text{平方米} = 10.0952 , text{平方米} ] 这与题目中的面积值相匹配。 结论 通过上述步骤,我们可以看到,如果一个正方形的面积是10平方单位,那么它的边长大约是$sqrt{10}$米。这个推导过程不仅涉及了几何学的基本知识,而且还涉及到了比例和代数的基本概念。通过具体的实例,我们可以更直观地理解这个概念,并将其应用到现实生活中。
标签:#福地阅读网



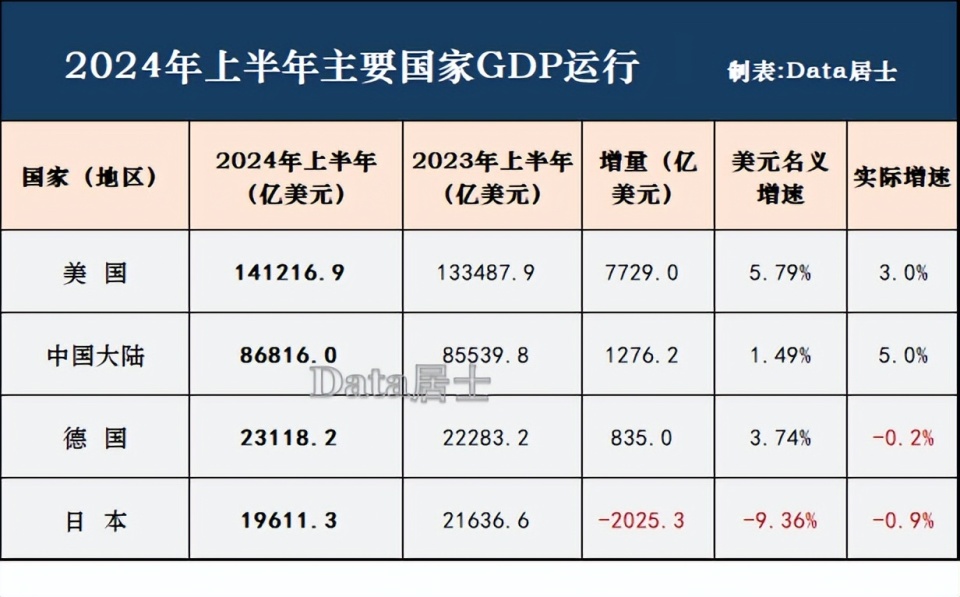


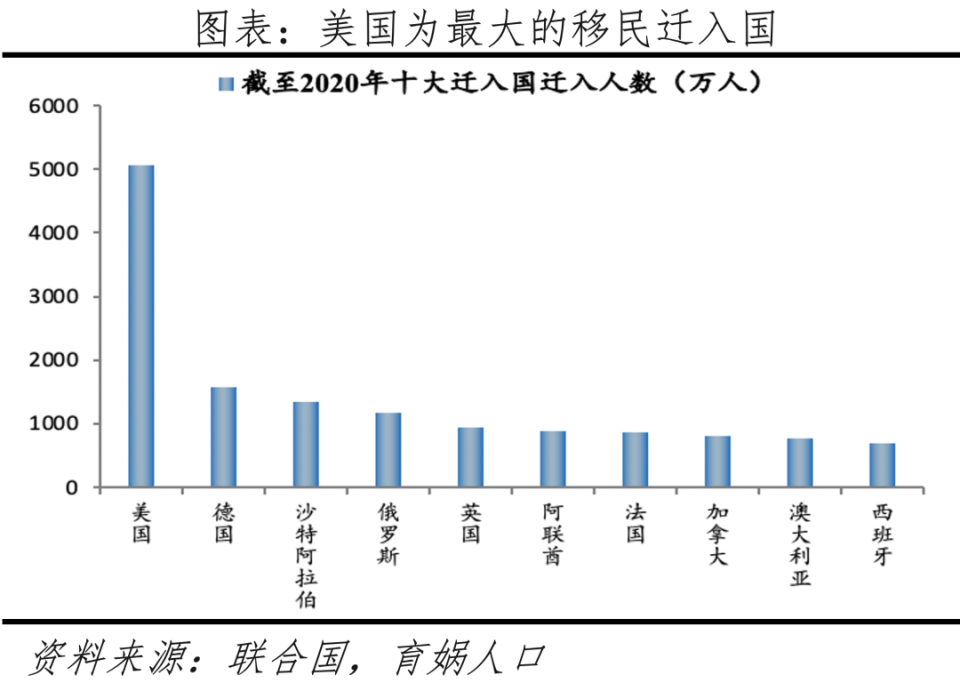

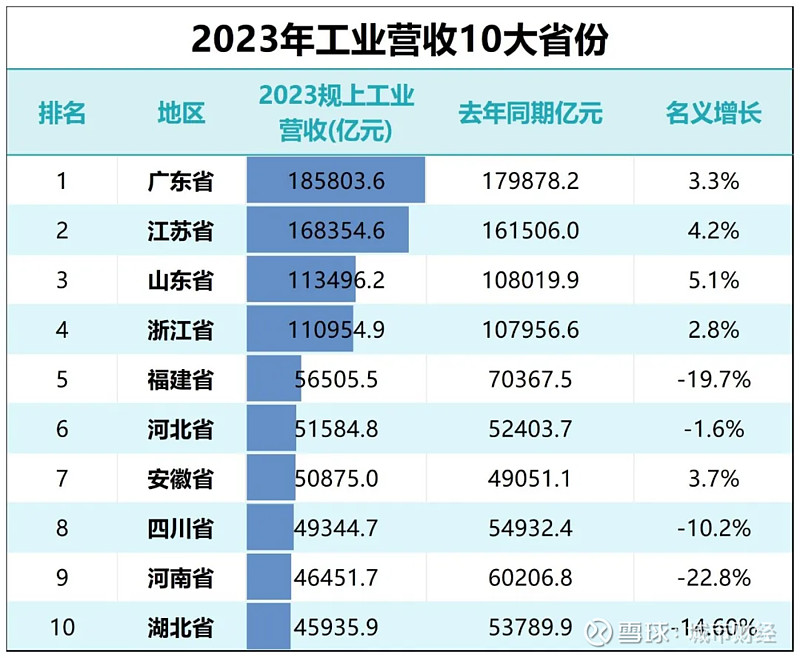



评论列表